Quantum Theory

• An effective solution to convex 1-body N-representability F. Castillo, J.-P. Labbé, J. Liebert, A. Padrol, E. Philippe, C. Schilling Ann. Henri Poincaré, 24, (2023), no. 7, 2241-2321.
• Foundation of one-particle reduced density matrix functional theory for excited states J Liebert, F. Castillo, J.-P. Labbé, C. Schilling J. Chem. Theory Comput., 18, (2022) no. 1, 124-140.

Discrete Geometry

• Lineup polytopes of products of simplices F. Castillo, J.-P. Labbé, Ann. Inst. Henri Poincaré Comb. Phys. Interact., (2024) in press.
• Congruence Normality of Simplicial Hyperplane Arrangements via Oriented Matroids M. Cuntz, S. Elia, J.-P. Labbé, Ann. Comb., 26, (2022) no. 1, 1-85.
• Combinatorial inscribability obstructions for higher-dimensional polytopes J. Doolittle, J.-P. Labbé, C. Lange, R. Sinn, J. Spreer, G.M. Ziegler, Mathematika, 66, (2020), no. 4, 927-953.
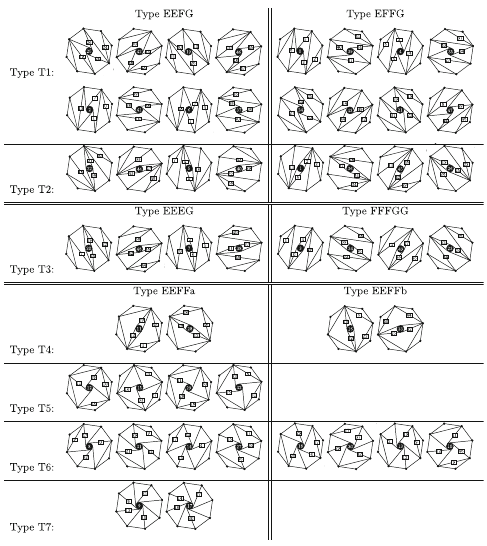
• Area difference bounds for dissections of a square into an odd number of triangles J.-P. Labbé, G. Rote, G.M. Ziegler, Exp. Math., 29, (2020), no. 3, 253-275.
• Fan Realizations of Type A Subword Complexes and Multi-associahedra of Rank 3 N. Bergeron, C. Ceballos, and J.-P. Labbé, Discrete Comput. Geom., 54 (2015), no. 1, 195-231.

Combinatorics of Simplicial Complexes

• Bounds for entries of γ-vectors of flag simplicial spheres J.-P. Labbé, E. Nevo, SIAM J. Discrete Math., 31, (2017), no. 3, 2064-2078.
• Hirsch polytopes with exponentially long combinatorial segments J.-P. Labbé, T. Manneville, and F. Santos, Math. Program., 165 (2017), no. 2, 663–688.

Geometric Group Theory / Coxeter Groups

• Limit directions for Lorentzian Coxeter systems H. Chen and J.-P. Labbé, Groups Geom. Dyn., 11, (2017), 469-498.
• On inversion sets and the weak order in Coxeter groups C. Hohlweg and J.-P. Labbé, European J. Combin., 55, (2016), 1-19.
• Lorentzian Coxeter groups and Boyd-Maxwell ball packings H. Chen and J.-P. Labbé, Geom. Dedic., 74 (2015), no. 1, 43-73.
• Asymptotical behaviour of roots of infinite Coxeter groups C. Hohlweg, J.-P. Labbé, and V. Ripoll, Canad. J. Math. 66 (2014), no. 2, 323-353.

Geometric Structures in Cluster Algebras

• Cluster Algebras of Type D4, Tropical Planes, and the Positive Tropical Grassmannian S.B. Brodsky, C. Ceballos and J.-P. Labbé, Beitr. Algebra Geom., 58, (2017), no. 1, 25-46. We use the combinatorics of pseudo-triangulations of the octogon to characterize the combinatorial types of generic tropical planes in the tropical projective space of dimension 5.

• Subword complexes, cluster complexes, and generalized multiassociahedra C. Ceballos, J.-P. Labbé and C. Stump, J. Algebraic Comb. 39 (2014), no. 1, 17-51. We provide an interpretation of finite cluster complexes and multi-triangulations using the combinatorics of subword complexes of Coxeter groups.

Combinatorics

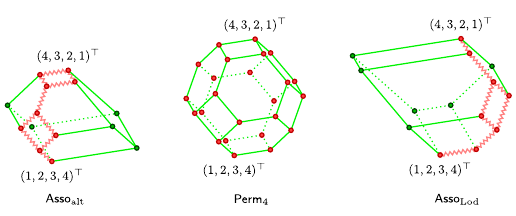
• Cambrian acyclic domains: counting c-singletons J.-P. Labbé, C. Lange, Order, 37, (2020), no. 3, 571-603. We provide lower and upper bounds for the number of common vertices of associahedra and permutahedra stemming from Hohlweg--Lange--Thomas' construction.

• Counting Types of Runs in Classes of Arborescent Words J.-P. Labbé and G. Labelle, Open Journal of Discrete Mathematics 3 (2013), no. 1, 7-15. We use species of structures to generalize the notion of runs in cointosses to general runs in arborescent words and obtain the generating series for various types of runs.
• Combinatorial variations on Cantor's diagonal S. Brlek, J.-P. Labbé and M. Mendès France, J. Comb. Theory, Ser. A 119 (2012), no. 3, 655-667. We use group actions in order to facilitate the enumeration of tableaux which are finite analogues of Cantor's famous diagonal argument.

Unpublished Preprints

A Perron theorem for matrices with negative entries and applications to Coxeter groups

J.-P. Labbé, S. Labbé, November 2015