Do polytopes play a role in Quantum Physics?
Yes, they do! Especially interesting is the fact that the Pauli Exclusion Principle can be expressed precisely using the hypersimplex. More precisely, the state of a system of N fermions is encoded into a thing called a density matrix. After applying a certain fundamental projection (called partial tracing) to obtain a smaller density matrix, the eigenvalues of the result have a very important physical interpretation: they indicate the expected number of particles found in a specific state. It turns out that it may be mathematically proven that these eigenvalues are between 0 and 1. The resulting set of possible spectra forms a polytope called hypersimplex.
In recent work with Julia Liebert, Christian Schilling, Federico Castillo, Eva Philippe and Arnau Padrol, we studied extensions to the Pauli Exclusion Principle via convex relaxation of a famous problem in Quantum Chemistry called the N-representability problem. It turns out that convex geometry and combinatorics play a capital role in establishing the foundation of the theory surrounding this extension. Incredibly, we obtain restrictions on bosonic systems, where no such Exclusion Principle was ever formulated.
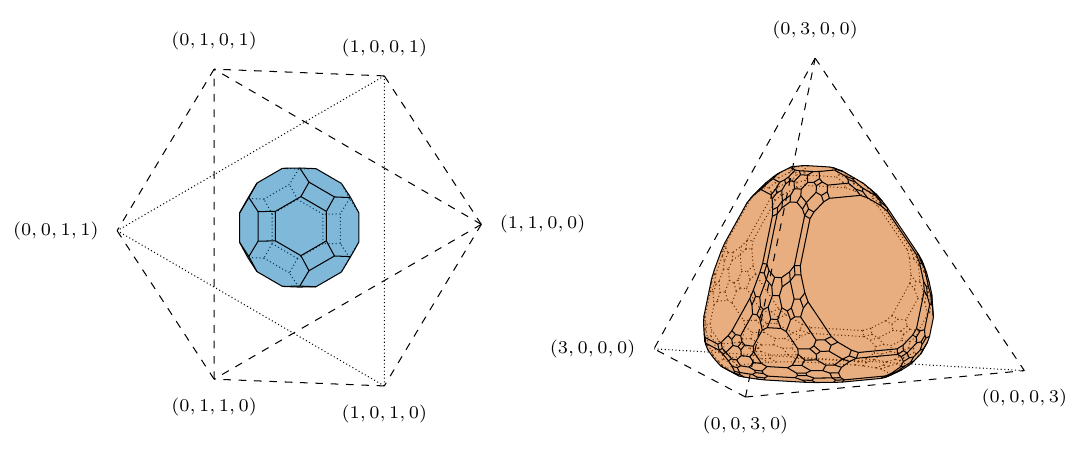
In the above picture, we see two polytopes. The polytope of the left represents the possible spectra of a system of 2 fermions in 4 orbitals coming from certain ensembles of states. On the left, the possible spectra of a system of 3 bosons in 4 orbitals coming from certain ensemble of states.
The details of this project can be found in the articles
- Ensemble reduced density matrix functional theory for excited states and hierarchical generalization of Pauli's exclusion principle C Schilling, S. Pittalis, Phys. Rev. Lett. 127, 023001
- Foundation of one-particle reduced density matrix functional theory for excited states J Liebert, F. Castillo, J.-P. Labbé, C. Schilling J. Chem. Theory Comput., accepted, 2021
- An effective solution to convex 1-body N-representability F Castillo, J.-P. Labbé, J. Liebert, A. Padrol, E. Philippe, C. Schilling, May 2021
Comments